…
终于还是想写一篇博客,这大概会记录一些我最近写的题吧。
这可能是我退役前的最后一篇博客了…
也可能是一篇类似日记的东西,反正也没啥人看。
如果我不咕咕咕的话,这篇博客到省选前都是会稳定更新的吧(大概)。
4.3
最近在家里呆太久了,什么事情都不想干,提不起劲来。。
考虑到我已经浪费了太多时间了,于是决定写一个日记,以此督促自己多干点事。。。
「USACO 2019.12 Platinum」Greedy Pie Eaters
假定每一个区间都有一只牛,只不过有些区间贡献为 $0$ ,那么最优策略一定是每头牛吃一个东西,调整法可证。
考虑区间 $\rm dp$ ,枚举区间 $(l,r)$ 最后一个被吃的东西 $k$ ,那么 $f_{l,k-1}+f_{k+1,r}+\max_{l\leq x\leq k\leq y\leq r} a_{x,y}\to f_{l,r}$,随便写一下就行了。
code。
「USACO 2020.2 Platinum」Equilateral Triangles
显然我们可以找到一个点,使得它到三角形三点相等。
这个点必然是这样的:
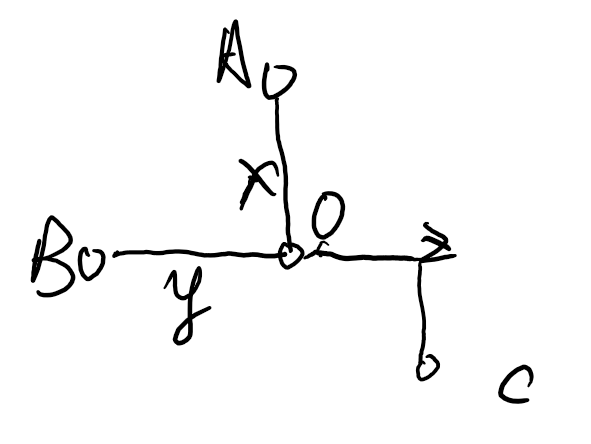
而且 $x=y=z$ ,画画图就能知道了(也有可能是旋转了若干个 $90^\circ$ )。
所以我们枚举 $O$ 点,枚举 $x$ 的长度,枚举四种情况,然后统计有多少个 $C$ 点合法即可,可以用前缀和优化(斜着统计前缀和),复杂度 $O(n^3)$ 。
注意特判一下 $C,O,A(B)$ 共线的情况,这种情况可能会算重复。
code。
4.4
「USACO 2019.12 Platinum」Bessie’s Snow Cow
开 $m$ 个 $\rm set$ 维护区间,线段树维护每个点的答案即可。
code。
「USACO 2019.12 Platinum」Tree Depth
首先,一个 $n$ 阶排列的逆序对的生成函数是 $\prod_{i=1}^{n}\sum_{j=0}^{i-1}x^i$,其中 $x^k$ 的系数表示逆序对为 $k$ 的方案数。
考虑假设当前有 $x$ 个数,往最后新加一个数,那么可能贡献 $0\cdots x$ 个逆序对。
计算笛卡尔数深度的期望时,可以考虑计算每个点是当前点祖先的概率之和。
假设 $i$ 是 $j$ 的祖先,意味着 $a_i$ 是 $[i,j]$ 的最小值(这里假定 $i<j$ ,另一种情况同理)。
那么我们枚举 $i,j$ ,首先我们把 $[i+1,j]$ 填入,然后再填入 $i$ ,此时我们要求 $i$ 是最小的,也就是不会贡献逆序对,所以我们把 $j-i$ 这一项改成 $1$ 即可。(另一种情况会贡献 $i-j$ 个逆序对,所以要改成 $x^{i-j}$)。
所以我们只需要实现,每次给多项式除掉 $\frac{x^k-1}{x-1}$ 或乘上 $\frac{x^k-1}{x-1}$ ,这个可以 $O(l)$ 实现( $l$ 是多项式长度)。
所以总复杂度就是 $O(n^3)$。
code。
4.6
「JOISC 2020 Day2」有趣的 Joitter 交友
并查集缩强连通块,对于每个块用 $\rm set$ 统计信息,合并的时候加个启发式合并,复杂度 $O(n\log n)$ 。
画画图就知道了(
code。
4.7
「JOISC 2020 Day4」首都城市
这题。。。我一开始想了个 $O(n\log n)$ 的做法。。特别难写,调了好久好久。。
然后我没调出来,冷静了一下之后想了一个很简单写的做法。。而且复杂度是 $O(n)$ 。
首先考虑如果我们对于颜色 $c$ ,所有这种颜色的点拿出来建一棵虚树,那么新建一个图,这个颜色向所有树边上的颜色连边,最后跑强连通分量,没有出度的连通分量去个最小值即可。
考虑怎么建这个图,我一开始很暴力的想,直接倍增建图,这种方法应该是可行的,但是细节特别多。。
换种方式考虑,对于点 $x$ ,考虑他的父亲 $fa_x$ ,如果 $x$ 不是虚树的根节点,那么显然要连边 $c_x\to c_{fa_x}$(重边自环无所谓)。
然后考虑,如果 $fa_x$ 是虚树 $c_{fa_x}$ 的根节点,那么显然一个答案更小的解是去合并 $fa_x$ 而非合并 $x$。
否则 $fa_x$ 会继续连向他的父亲,这样建出来的图可能会忽略掉一些较大的答案,但最小的一定能找到。
复杂度 $O(n)$ (而且这个代码目前是 $\rm loj$ 跑的最快的)。
code。
4.8
「JOISC 2020 Day2」变色龙之恋
考虑点 $p$ 和谁参加会议只会得到一种颜色,假设 $x$ 可以,那么我们连边 $p,x$。
可能的情况有:他喜欢的人 $x$ ,喜欢他的人 $y$,和他同色的人 $z$ 。
若 $x=y$,那么只有 $z$ 会和他连边,这时候不需要判断。
否则,会有三人和他连边,并且如果询问集合 $\{p,y,z\}$,答案为 $1$ ,其他的所有可能答案都不为 $1$。
所以通过这种方式可以找到每个人喜欢谁,进而得出答案。
如果暴力的算,需要询问 $O(n^2)$ 次。
我们考虑从前往后算谁和他连边,假设算到 $i$ 了,那么由于原图是二分图,点 $1\sim i-1$ 一定可以分成两个独立集,我们在每个独立集里二分询问即可。独立集可以用并查集维护。
大概需要询问 $3n\log n+6n$ 次,然后进行毁灭性的卡常,可以做到询问 $18000$ 次左右。
code。
「ARC070F」HonestOrUnkind
(今天听讲题听到的题,感觉特别有意思就写了下)
首先如果 $b\geqslant a$ 就无解,因为这 $b$ 个人中可以分出 $a$ 个装作诚实的人来演你,也就是说这 $a$ 个人城市,其他人不诚实。
考虑怎么找出一个诚实的人,我们维护一个栈,从 $1$ 到 $n$ 扫描:
- 如果栈是空的,当前点入栈。
- 否则询问栈顶,当前点是否诚实,如果回答诚实则入栈。
- 否则弹出栈顶,扫描下一个点。
容易发现,如果有一个诚实的人入栈,后面的人都诚实。
并且最多就是一个诚实的人和一个不诚实的抵消,那么最后一定会剩下一个诚实的。
所以最后栈顶是诚实的。共询问至多 $2n$ 次。
code。
CF1332E. Height All the Same
这 $\rm Div.2E$ 居然还蛮有意思的。
首先对于一个状态,对于每个点能减二就减二,那么最后会剩下一个 $0,1$ 矩阵。
考虑怎样的 $0,1$ 矩阵是合法的,我们考虑把一堆横着的多米诺骨横着首尾相叠放在一排,那么首尾是 $1$ ,其余多出来的是 $2$ ,这样我们可以把任意两个纵坐标相同的点加一,竖着的同理。
所以我们可以把任意两个点加一。
所以一个 $0,1$ 矩阵不合法,当且仅当 $0,1$ 的个数都为奇数。
所以如果一开始 $nm$ 为奇数,所有情况都合法。
否则考虑枚举偶数位置有几个,设 $x$ 为 $[l,r]$ 奇数个数, $y$ 为偶数个数,答案就是:
算一下就好了。
code。
4.9
开了场 $\rm CF$ ,比赛链接。
CF1329A. Dreamoon Likes Coloring
构造题,很简单就不说了(
code。
B. Dreamoon Likes Sequences
有一个比较简单的性质:假设 $x$ 最高位为 $f(x)$ ,那么一个序列满足条件至少要保证 $f(a_i)<f(a_{i+1})$。
并且如果这个条件满足,那么显然 $b$ 数组也会严格上升。
那么答案就是,把所有最高位为 $x$ 的方案数加一乘起来,最后减去空串,这是比较基础的组合计数。
复杂度 $O(\log n)$ 。
C. Drazil Likes Heap
考虑 $g$ 树上的点 $x$ 最小可以选啥,显然要满足这俩条件:
- 在 $x$ 子树内。
- 权值大于 $x$ 儿子的最大值。
显然我们可以贪心的选满足条件的最小的。
那么从下到上拿个东西合并一下就行,最后我们按编号从大到小删除不需要的即可(这样先删的不会对后删的造成影响)。
我一开始拿 $\rm set$ 暴力合并过不了。。得拿 $\rm vector$ 写个类似归并排序的玩意才能做到 $O(n\log n)$。
code。
4.10
D. Dreamoon Likes Strings
首先我们把所有 $s_i=s_{i+1}$ 的位置拉出来,叫做 $t$ 数组,并记录 $c_x$ 表示 $s_{t_i}=x$ 的位置数。
显然我们每次可以消掉 $t_i+1\sim t_{i+1}$ 的这些字符,然后删去 $t_i,t_{i+1}$ ,但是如果 $s_{t_i}=s_{t_{i+1}}$ ,那么不能删去 $t_i$。
所以我们显然是要多做前面的那种操作。
于是有了一个贪心做法:
- 首先我们维护一个栈,按顺序加入 $t_i$ ,如果一旦满足 $\max c_i\geqslant \dfrac{\sum c_i}{2}$ 立刻退出此过程,否则:如果 $t_i$ 颜色和栈顶相同,$t_i$ 入栈,否则消去栈顶和 $t_i$ (如果栈为空直接入栈)。(这个过程可能不会进行)
- 那么此时一定有一个东西个数大于等于全部的一半,我们新开一个栈,和上面的过程差不多,只是要求栈顶或 $t_i$ 有且仅有一个颜色等于最大的那个才消去。
- 那么最后一定剩下了若干个相同的颜色,每次消去一个即可。
复杂度可以做到 $O(n)$ ,但是我用了一个线段树来维护。。所以我的代码复杂度为 $O(n\log n)$。
code。
4.11
我突然发现前面没给题目链接(
但是有代码链接本质相同(
你可以点一下代码再转到题目页面 [呲牙]
CF1333F. Kate and imperfection
假设 $S=\{a_1,\cdots,a_k\}$ 是一个最小代价的集合,我们找到最大 $\gcd$ 的二元组 $(a_x,a_y)$ ($a_x<a_y$),那么 $a_x$ 如果不是 $a_y$ 的最大约数,那么我们肯定可以选一个更小的 $a_y$ 使得条件成立。
假设 $f(x)$ 表示不等于 $x$ 的最大约数,那么 $S$ 的代价就是 $\max f(a_i)$。
所以我们求出所有 $f(i)$ ,排一遍序就做完了。
code。
CF1320A. Journey Planning
一句话题。。code。
B. Navigation System
反图求最短路。code。
C. World of Darkraft: Battle for Azathoth
第一维排序去掉,线段树维护第二维即可。
code。
4.12
打了一天的摆子。。。
晚上打了场 $\rm cf$ ,被我打成找规律场了。。。找规律过了 $\rm B,C$ ,还加了 $\rm 25$ 分。
比赛链接。
4.13
补了下昨天的 $\rm D$ 。
CF1338D. Nested Rubber Bands
大概就是说,我们选出一些点来连接圈圈,然后所有这些点相邻的点就是那些圈圈,其他的点都用不上。
假设链接的点叫红点,显然这些红点一定分布在某两个点的路径上,并且相邻两个点的距离不超过 $2$ ,否则我们可以把中间那个也弄成红点,一定不劣。
那么搞个 $\rm dp$ 就行了,复杂度 $O(n)$ 。
code。(这代码为了少写两句话写的比较奇怪。。但是正确性应该是可以保证的)
别问 问就是懒得写了